Measurement and modeling of indoor radon concentrations in residential buildings
Article information
Abstract
Radon, the primary constituent of natural radiation, is the second leading environmental cause of lung cancer after smoking. To confirm a relationship between indoor radon exposure and lung cancer, estimating cumulative levels of exposure to indoor radon for an individual or population is necessary. This study sought to develop a model for estimate indoor radon concentrations in Korea. Especially, our model and method may have wider application to other residences, not to specific site, and can be used in situations where actual measurements for input variables are lacking. In order to develop a model, indoor radon concentrations were measured at 196 ground floor residences using passive alpha-track detectors between January and April 2016. The arithmetic mean (AM) and geometric mean (GM) means of indoor radon concentrations were 117.86±72.03 and 95.13±2.02 Bq/m3, respectively. Questionnaires were administered to assess the characteristics of each residence, the environment around the measuring equipment, and lifestyles of the residents. Also, national data on indoor radon concentrations at 7643 detached houses for 2011-2014 were reviewed to determine radon concentrations in the soil, and meteorological data on temperature and wind speed were utilized to approximate ventilation rates. The estimated ventilation rates and radon exhalation rates from the soil varied from 0.18 to 0.98/hr (AM, 0.59±0.17/hr) and 326.33 to 1392.77 Bq/m2/hr (AM, 777.45±257.39; GM, 735.67±1.40 Bq/m2/hr), respectively. With these results, the developed model was applied to estimate indoor radon concentrations for 157 residences (80% of all 196 residences), which were randomly sampled. The results were in better agreement for Gyeonggi and Seoul than for other regions of Korea. Overall, the actual and estimated radon concentrations were in better agreement, except for a few low-concentration residences.
INTRODUCTION
Radon, which is the primary constituent of natural radiation, is the second leading environmental cause of lung cancer after smoking [1,2]. To confirm a relationship between indoor radon exposure and lung cancer, retrospective assessment of exposure to radon for an individual or selected population must be performed. However, determining to how much radon an individual has been exposed over their lifetime can be difficult due to a lack of available information on indoor radon concentrations. Thus, estimating indoor radon levels of residences is often necessary. In this paper, we propose a model for estimating indoor radon concentrations.
Indoor radon is affected by several parameters, all of which can vary from residence to residence, such as local geology, building design, meteorological patterns, and inhabitant behavior. Several studies have attempted to estimate indoor radon concentrations with mathematical models under site-specific conditions: Arvela et al. [3] estimated indoor radon concentrations with a mathematical model for measured variations in Finnish dwellings. Font Guiteras [4] and Font and Baixeras [5] developed the radon generation, entry, and accumulation indoors model, which describes all known sources of radon and is adapted to Mediterranean climate houses and Swedish houses [6,7]. Man and Yeung [8] and Shaikh et al. [9] have calculated indoor radon concentrations in high-rise buildings. Ramola et al. [10] estimated indoor radon concentration based on radon flux in soil and groundwater. These developed models and applications were previously reviewed by Park et al. [11].
As stated above, previous studies were developed under sitespecific conditions and required many information on input variables. In this paper, we sought to develop a model for estimating indoor radon concentrations. This model might have wider application to other residences, not to specific site, and could be used in situations where actual measurements for input variables were lacking. First, we constructed a model based on theories suggested by Arvela et al. [3] and Font Guiteras [4]. The model was developed to account for four main factors affecting indoor radon concentrations: soil, building materials, the outdoor air, and ventilation. When adapting a model to real inhabited residences, however, it is quite difficult, or rather impossible, to collect actual data on these parameters for all inhabited residences. Thus, we utilized national survey data on indoor radon concentrations at detached houses and meteorological data in order to estimate parameters lacking information using special codes in MATLAB R2012b (MathWorks, Seoul, Korea). Then, we considered ratio mean values of the estimated parameters as representative values. Overall, actual and estimated radon concentrations showed similar trends, except for a few residences.
METHODS
Materials
Actual indoor radon concentrations were measured at 196 ground floor residences using passive alpha-track detectors (Raduet Model RSV-8; Radosys Ltd., Budapest, Hungary) between January and April 2016 over a minimum of 90 days (arithmetic mean [AM], 117.86 ± 72.03 Bq/m3; geometric mean [GM], 95.13 ± 2.02 Bq/m3). The residents were recruited voluntarily from different cities and counties of Gangwon, Gyeonggi, Gyeongnam and Seoul. The radon concentration values were obtained in two different rooms of each residence, choosing among living rooms, bedrooms, or spaces where residents mainly spend most of their time. We used the GMs of radon concentrations indoors from two points in the residence due to the lognormal distribution of radon concentrations.
Along with the physical measurements, questionnaires were also administered to assess characteristics of each residence (region, type of house, foundation of the house, usage of underground space, construction year, use of gypsum board, and building materials for the floor and walls), the environment around measuring equipment (positioning of radon measuring equipment and nearby windows and cracks), and the lifestyles of the residents (number of residents, frequency of ventilation, heating period, and use of groundwater).
Also, we utilized national data on indoor radon concentrations for the winter season from 2011 to 2014, which were obtained during a special measurement campaign for select houses in Korea using passive alpha-track detectors (Raduet Model RSV-8) [12]. We extracted 7643 measurements taken at the main living room of each detached house (AM, 146.67±163.63 Bq/m3; GM, 104.31±2.19 Bq/m3). These data were used to estimate the radon concentrations in the soil and outdoor air.
Ventilation is a major factor affecting indoor radon concentrations [13]. Ventilation rates depend on meteorological factors, such as indoor-outdoor temperature differences and wind speed. We obtained the average temperatures and average wind speeds of each region during the measuring period from the National Climate Data Service System (NCDSS) [14]. Meteorological data on temperature and wind speed were used to estimate ventilation rates. Therefrom, we developed a mathematical model of indoor radon concentrations.
Indoor Radon Model
The indoor radon concentrations were based on the following mass balance equation [3-10, 13,15-17]:
Indoor radon accumulation=radon entry±radon exchange–decay reaction
In general, the soil is the primary source of radon entry, followed by building materials [18]. Radon in the soil permeates a building by diffusion and advection mechanisms. Radon in building materials also enters by diffusive transfer. Since radon entry from the soil primarily affects indoor radon levels in low-rise residences, the present model was designed around radon entry from the soil and building materials.
With the above assumptions or simplifications, we modified a model based on theories suggested by Arvela et al. [3] and Font Guiteras [4]. As stated above, the model was developed to account for soil, building materials, the outdoors, and ventilation. The following system of differential equations was obtained:
where Cbm = radon concentrations in building materials (Bq/m3), Ci = indoor radon concentrations (Bq/m3), Cs = radon concentrations in the soil (Bq/m3), Co = radon concentrations in outdoor air (Bq/m3), Ebm = effective radon exhalation rate of building materials (Bq/m2/hr), Es = effective radon exhalation rate of soil (Bq/m2/hr), ka = advection transfer coefficient of soil (m/Pa/hr), kd,bm = diffusion transfer coefficient of building materials (m/hr), kd,s = diffusion transfer coefficient of soil (m/hr), Sbm = indoor surface area of radon containing building materials (m2), Sg = building area towards the ground (m2), V = volume of the indoors (m3), λ = radon decay constant (hr), λv = ventilation rate (hr), and ∆Ps-i = soil-indoor pressure difference (Pa).
The model takes into account several important factors. First, equation (1) describes the rate of change in indoor radon concentrations attributed to radon entry, radon exchange caused by ventilation, differences in indoor and outdoor radon levels, and decay. The first term in the right hand side of equation
describes radon entry from the soil via diffusive and advective flow. These are caused by differences in radon concentrations between the soil and the indoor space and pressure differences between the soil and indoor space, respectively. The second term in the right hand side of equation
describes the diffusive flow caused by difference in radon concentrations between building material and the indoor space. The third and last terms in equation
describe radon exchange and reaction caused by ventilation and radioactive decay, respectively.
Equations (2) and (3) describe the rate of change in radon concentrations in the soil and building materials, respectively. The first terms in the right hand side of equations (2) and (3) take into account the radon flow exhaled from the soil and building material, respectively. The second terms in the right hand side of equations (2) and (3) describe the radon flow caused by the transfer mechanisms between the indoor space and radon sources (soil and building material, respectively). The last terms in equations (2) and (3) describe radon reactions caused by radioactive decay in the soil and building material, respectively.
Since it is hard to measure the ventilation rate for each residential, it can be estimated with a simple model using information about the frequency of opening windows in a room and meteorological factors, such as indoor-outdoor temperature difference and wind speed. Modifying a model described in Arvela et al. [3], we calculated ventilation rates by the following equation:
where ft, fw = fitting parameters, Ti, To = indoor and outdoor temperatures, respectively (˚C), u = wind speed (m/sec), N = the number of ventilations (dimensionless), p = fitting parameter (0 < p < 1). In this paper, we may assume that fitting parameter p in equation (4) equals 1/2.
After finding the steady state solution of the above system of differential equations, we arrived at the following equations for estimating indoor radon concentrations:
Model Application
For application of the model, we noted that a large number of input parameters would be needed to obtain the indoor radon concentration, and since most of these input values are specific to the residence, they are not readily available to the general user. In instances where the measured value of a parameter is available, one can simply use the value in the equation. Otherwise, one would need to use a semi-empirical manner or reported literature values. Moreover, some of the parameters are considered as fixed values, while others are modeled as certain mathematical functions. The following numerical inputs are required in equation (5).
Determination of radon concentrations in the soil and building materials
Since radon in the soil is the main source of indoor radon, especially in ground floor residences, one may think that indoor radon concentrations are more dependent on those in soil than building materials. Furthermore, the cumulative radon concentration for soil and building materials may be assumed to equal radon concentration in soil (Cs+Cbm≈Cs), since radon concentrations in building materials are relatively small, compared to radon concentrations in soil (Cs≫Cbm), in general.
However, even if radon levels in soil are measured, they are only measured at a particular time point. Therefore, it is inevitably imperfect to take measured values as representative values. Figure 1 shows the measured indoor radon concentrations (n = 196) in comparison to national data (n = 7643) by region.
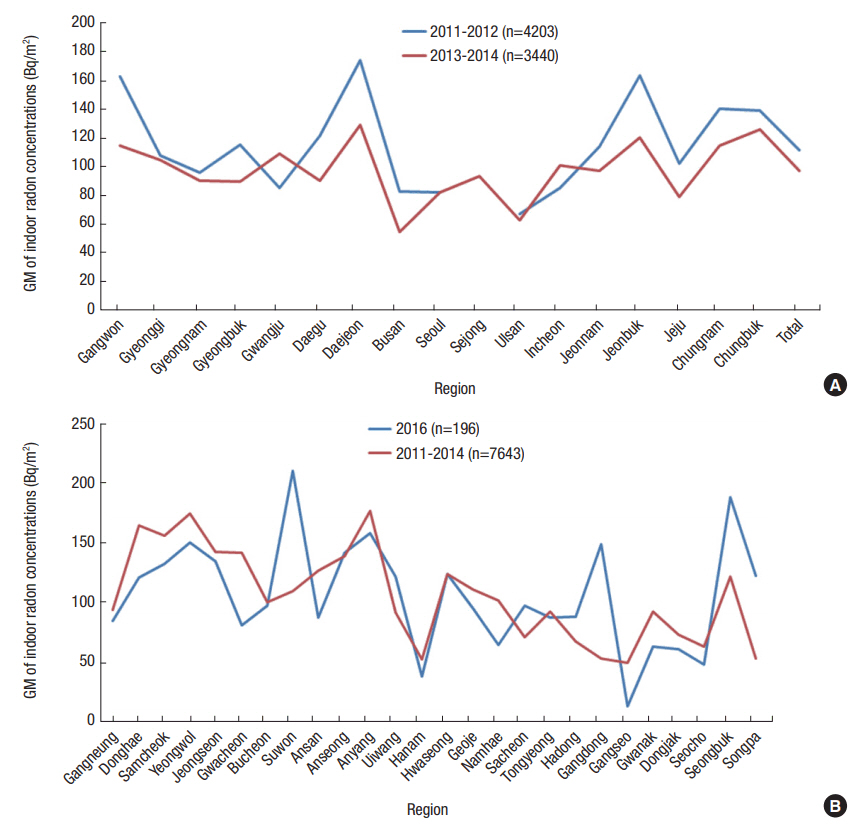
Comparison of indoor radon concentrations (A) 2011-2012 (n=4203) and 2013-2014 (n=3440), (B) 2016 (n=196) and 2011-2014 (n=7643). GM, geometric mean.
Except for a few regions, the radon concentrations are similar. This is to be expected since, as we stated earlier, radon in the soil is the main source of indoor radon. Therefore, we estimated the radon concentrations in soil according to administrative districts using national data on indoor radon concentrations at detached houses (n=7643) for 2011-2014. In detail, we assigned weights on each region based on the ratio of the regional GM to total GM 104.31 Bq/m3. Table 1 gives the estimated values for radon concentrations in the soil based on the regional weights and the results of soil radon concentrations in study area of Gwanak-gu in Seoul, as reported by Chon [19].
Determination of radon concentrations in outdoor air
Available information on radon concentrations in outdoor air is also limited. Moreover, this variable strongly depends on radon in soil. For radon concentrations in outdoor air, we also assigned estimated values by administrative district in the same way as that for soil. Table 1 shows that estimated values are quite similar to measured values of radon concentrations in outdoor air, as reported by Zhuo et al. [20].
Determination of the effective radon exhalation rate of building materials
The effective radon exhalation rates for concrete and cement have previously been reported by Lee et al. [21] (see also [22] for more details).
Determination of the size of a building
The size of a building was not measured in this study. Some constant values have been assigned to the input variables to account for the size of a building under some assumptions: the values of the ground surface to indoor volume ratio Sg/V and indoor surface to indoor volume ratio Sbm/V are chosen on the basis of a floor height of 2.4 m.
Determination of meteorological variables
To estimate ventilation rate, we used outdoor temperature and wind speed values reported directly from NCDSS. Table 1 lists the average temperatures and wind speed of each region during the measuring period. Furthermore, we assumed that indoor temperatures in the winter were 20˚C, which is the recommended temperature during the winter in Korea.
Determination of radon decay
The radon decay constant is 2.098 × 10-6/sec [23].
These assumptions give the following equation (6):
Parameter Estimation
For ground residences, indoor radon concentrations are mainly affected by radon flow from soil and ventilation. However, information about the effective radon exhalation rate of soil in Korea is lacking, and it was difficult to assign values to a few parameters, such as radon concentrations in soil. Moreover, there were many uncertainties on radon flow from the soil and ventilation rates. Therefore, we estimated the effective radon exhalation rate of soil in equation (6) for each residence.
Meanwhile, we used equation (4) for estimating ventilation rates, more precisely, after estimating the fitting parameters ft and fw in equation (4). To obtain reasonable values of the ventilation rate, we estimated fitting constants within the range from 0.1 to 1/hr for ventilation rate (typical infiltration rates referred to in Nazaroff et al. [24]).
We estimated parameters for the whole data set (n = 196) and with the input variables using special codes, such as ‘fmincon’ and ‘fminsearch’, developed in MATLAB R2012b. Moreover, a random sample (n = 157) was also utilized for mutual comparison.
RESULTS
Results of Parameter Estimation
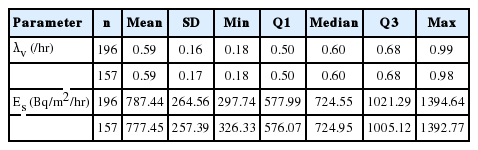
The estimated fitting parameters ft and fw were 0.03 and 0.06, respectively. The estimated ventilation rate and effective radon exhalation rate from the soil varied from 0.18 to 0.98/hr (0.59 ± 0.17/hr) and 326.33 to 1392.77 Bq/m2/hr (AM, 777.45 ± 257.39; GM, 735.67 ± 1.40 Bq/m2/hr), respectively. Table 2 shows the results of estimating parameters for the whole data set (n = 196) and a random sample (n = 157), respectively.
Next, we applied these results to estimate indoor radon concentrations. To do this, the values of all input variables in the model concerning the specific characteristics and surroundings of the residence were necessary. Thus, we considered GM values of the estimated effective radon exhalation rates from the soil by administrative district (Table 3).
Application to Other Residences
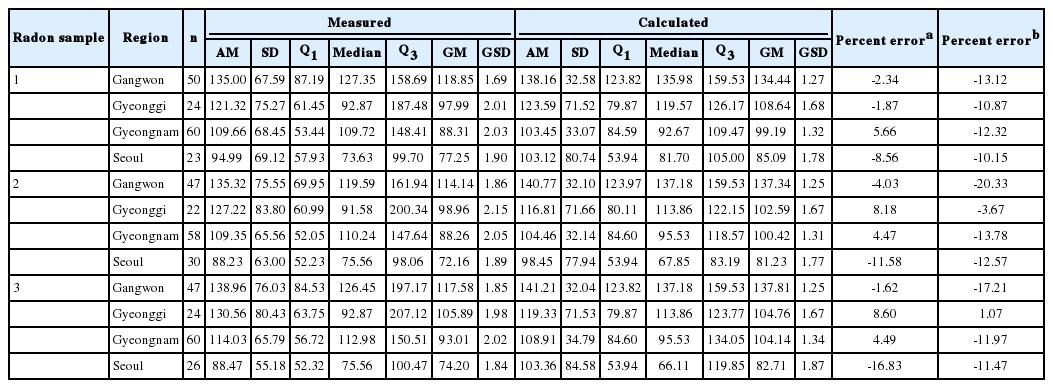
With the results achieved so far, the model was applied to estimate indoor radon concentrations for 157 residences (80% of all 196 residences), which were randomly sampled. A comparison between the actual and estimated indoor radon levels for each residence is shown in Figure 2 and Table 4.
Since the indoor radon concentration is log-normally distributed, the actual and estimated radon concentrations were in better agreement for Gyeonggi and Seoul than other regions based on the quartile information. The estimated effective radon exhalation rates from the soil Es, one of the important variable of our model, might be well fitted for Gyeonggi and Seoul. This is likely because the artificial and nature environments are more uniform in Gyeonggi and Seoul than other regions. On the other hand, it was thought that resident’s incorrect response to frequency of ventilation caused large estimation error because ventilation rate was another important variable of our model. Overall, the actual and estimated radon concentrations were in better agreement, except for a few low-concentration residences.
DISCUSSION
In this study, we successfully developed a mathematical model for estimating indoor radon concentrations. While this model is not sufficient to cover the entire transfer of radon, our method is advantageous in situations where actual measurements for input variables are lacking. Under the mathematical and physical hypotheses, measured and published data were utilized to estimate parameters. The effective radon exhalation rates from the soil Es were estimated and might be well fitted for Gyeonggi and Seoul. This is likely because the artificial and nature environments are more uniform in Gyeonggi and Seoul than other regions. Also, a model of ventilation rate was developed. We estimated the ventilation rates using resident’s responses to frequency of ventilation without other measurement values. However, since ventilation rate was another important variable of our model, resident’s incorrect response to frequency of ventilation could cause large estimation error. Further studies needed to consider other measurable parameters instead of resident’s response to frequency of ventilation for better model performance. Despite the limitations mentioned above, we considered the several important factors such as the radon in soil and ventilation rate. In consequence, the actual and estimated radon concentrations were in better agreement overall, except for a few low-concentration residences.
The model developed in this study may be applied as a tool for estimating indoor radon concentrations with realistic parameter values. Considering the lack of available information input variables, further studies should seek to analyze additional factors such as radon exhalation rates or radon concentrations in the soil and ventilation rates for better model performance. Meanwhile, our model may be improved considering a random effect model designed to account for unknown factors and measurement error.
Acknowledgements
This study was supported by the Korean Ministry of Environment as part of the “Environmental Health Action Program” (grant no. 2015001350002).
Notes
The authors have no conflicts of interest associated with the material presented in this paper.